Цифровой закон идеальных пропорциональных соотношений человеческого тела – Вопрос: Какой скульптор в сочинении Канон вывел закон идеальных пропорциональных соотношений тела человека? : Смотреть ответ

Какой скульптор вывел закон идеальных пропорций тела человека?

Скульптор Поликлет в своём произведении «Канон» в V веке до нашей эры разработал и описал систему идеальных пропорций человеческого тела.

Он стремился точно определить пропорции человеческого тела, согласно со своими представлениями об идеале.

Вот результаты его вычислений: голова — 1/7 всего роста, лицо и кисть руки — 1/10, ступня — 1/6. Однако уже современникам фигуры Поликлета казались слишком массивными, «квадратными». Тем не менее каноны стали нормой для античности и с некоторыми изменениями для художников ренессанса и классицизма.

Канон Поликлета был воплощен им в статуе Дорифор («Копьеносец»). Статуя юноши полна уверенности; уравновешенность частей тела олицетворяет могущество физической силы. Широкие плечи почти равны высоте туловища, половина высоты тела приходится на лонное сращение, высота головы восемь раз укладывается по высоте тела, а центр «золотой пропорции» приходится на уровень пупка.

Написать комментарий

Данная запись опубликована в 23.12.2016 20:43 и размещена в Кто хочет стать миллионером. Вы можете перейти в конец страницы и оставить ваш комментарий.

Мало букафф? Читайте есчо !

Какое дерево бывает черным, белым и пирамидальным?

Ноябрь 13, 2015 г.

Ответ — тополь. Известно множество разновидностей Тополя (Populus). Насчитывается около 35 видов род быстрорастущих, короткоживущих этих деревьев семейства ивовых (Salicaceae). Родина тополя – северное полушарие, где тополи произрастают от Арктики …

Читать

Остров, на котором находится вулкан Этна?

Январь 3, 2013 г.

Вергилий считал, что циклопы живут в горе на острове Сицилия. И гора эта – знаменитый на весь мир вулкан Этна. В мифах же рассказывалось, что богиня Афина в битве богов с гигантами придавила горой бессмертного Энкелада. Время от времени он пытается освободиться …

Читать

Золотое сечение. Божественная пропорция | Журнал Ярмарки Мастеров

Золотое сечение (лат. Sectio aurea) — термин, знакомый многим. Освежим немного нашу память, друзья!

Золотое сечение, или золотая пропорция — идеальное соотношение величин, лежащее в основе гармонии природы и человека. «Золотое сечение» имеет массу удивительных свойств (из разряда «Ух, ты! Занимательная геометрия»), возможно, именно поэтому, ему приписывается некое божественное происхождение и ряд вымышленных свойств.

Если выражаться сухо по-научному, то ЗС — это соотношение величин или отрезков, при котором отношение большей части к меньшей равно отношению всей величины к большей части. Приблизительное округленное процентное соотношение частей — 62% и 38%.

Числовая величина золотого сечения – 1, 6180339887 (и это еще округление =)) до десятого знака!)

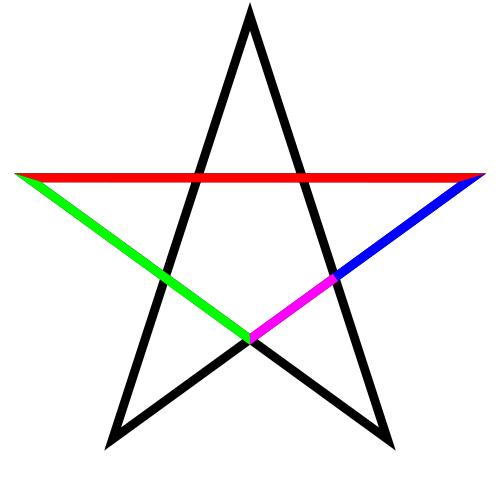
Пример золотого сечения в лучах пятиконечной звезды.

С Вашего позволения, я опущу многострочные математические фомулы и фомулировки =) Перейдем сразу к Прекрасному!

Зачатки этого понятия встречаются еще в античной литературе, датированной 300 гг. до нашей эры, а «божественная пропорция» широко применялась в трудах и работах мастеров Эпохи Возрождения. Иоган Кеплер, астроном 16 в. назвал золотое сечение одним из сокровищ геометрии. Он впервые обращает внимание то, как проявляется ЗС в ботанике (рост растений и строение стеблей и соцветий).

В середине 19 в. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение лежит в основе некой среднестатистической пропорции человеческого тела. Деление тела точкой пупка – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 к 8 = 1,625 и несколько ближе подходят к ЗС, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 к 5 = 1,6. Пропорции золотого сечения проявляются и в отношении всех частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.

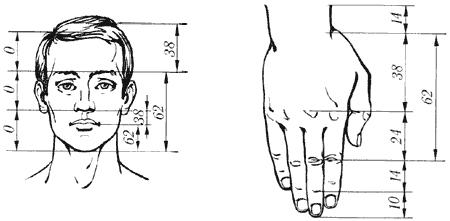
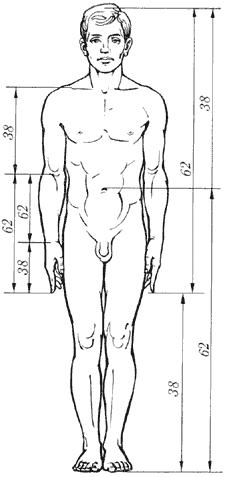
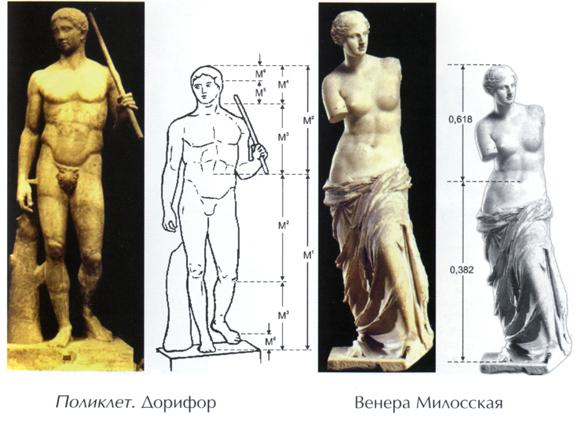
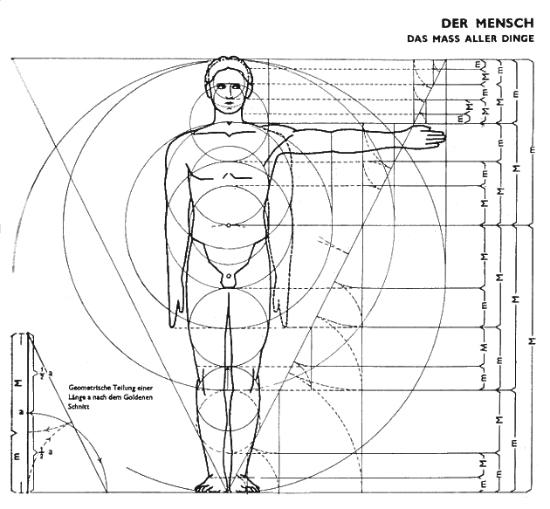
На протяжении веков существовало общеприянтое мнение, что рукотворные объекты, созданные с применением принципа ЗС, воспринимаются Человеком как наиболее гармоничные, совершенные. Пропорции золотого сечения можно выделить в проекциях египетских пирамид. Соотношение сторон плана Парфенона в Афинском Акрополе также являет собой не простое кратное число, а бесконечно дробное (догадайтесь, какое?). Таковыми же являются соотношение сторон планов и фасадов многих византийских церквей, романских готических соборов. Принято считать, что еще со времен Ренессанса многие художники и архитекторы сознательно используют принципы золотого сечения в своих творениях.

Золотое сечение на примере фасада храма Парфенона

Однако же, бытует и мнение, что значение ЗС в искусстве сильно преувеличенно, порой притянуто за уши исследователями, либо основано наошибочных расчетах. Тут каждый останется при своем. Помню, как на втором курсе в архитектурном нас, лопоухих, профессора пытались приобщить к прекрасному и долго-долго втолковывали про принципы золотого сечения в зодчестве, ряды Фибоначчи и прочее-прочее =)) Но настоящее понимание этой волшебной геометрии пришло ко мне много позже, при изучении бионики (один из стилей архитектуры), которая базируется именно на совершенстве природных форм. Согласитесь, мы не в силах оспаривать очевидное, а примеры идеальной пропорции встречаются сплошь и рядом: в раковинах аммонитов, в расположении ветвей на стебле растения, прожилках листьев. Ведь все, что приобретало какую-то форму, образовывалось, росло, осуществляло свое развитие в основном в двух вариантах – рост вверх или расстилание по поверхности земли и закручивание по спирали. Раковина закручена по спирали. И вообще, представление о золотом сечении будет неполным, если не сказать о спирали. Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали: увеличение ее шага всегда равномерно.

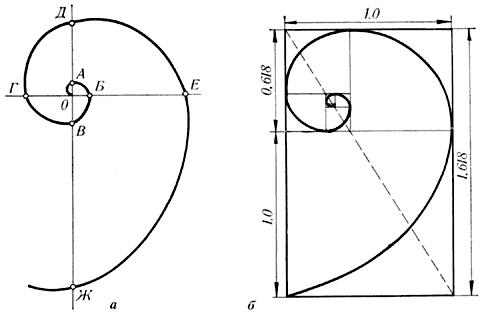
Спираль Архимеда

Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке , семян подсолнечника, шишек сосны проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНК закручена двойной спиралью. Гете называл спираль «кривой жизни».

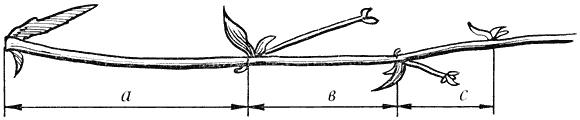
Стебель цикория

Полюбуйтесь, как наглябно иллюстрирует природа принципы Золотого сечения! Совершенные спирали без изъян, соотношения витков которых строго соответсвует канонам и принципам построения ЗС.

© Copyright: Tihomir Balkonskiy

© Copyright: Kibardindesign

Материалы взяты из Интернета.

Текст преимущественно авторский =)

Спасибо за Ваше внимание, Даша Самаркина

Идеальные пропорции тела человека — красота сквозь время

Представления о красоте тела у каждого человека свои. Для одних эталоном являются пышные формы, другие предпочитают четкость линий. При этом пропорции тела у всех людей разные и найти точную формулу пока не удалось даже величайшим умам всего человечества. Вместе с изменениями мира меняются и взгляды об идеале. Давайте попробуем проследить, как на протяжении истории менялись эти представления.

Первые изображения женщины относятся к эпохе палеолита, именно в то время появились первые статуэтки из камня. Короткое туловище, вздутый живот, гипертрофированная грудь, массивные бедра, маленькие руки и ноги – эти характеристики свидетельствуют о культе плодовитости женщин. Вместе с тем на

изображениях, которые относят к периоду египетской цивилизации, у женщин отмечается стройность, а идеал их красоты представлен высокой, стройной брюнеткой, которая имеет атлетическое телосложение (плечи широкие, плоские грудь и бедра, длинные ноги).

В пятом веке до нашей эры скульптор Поликлерт разработал канон, систему, которая описывала идеальные пропорции тела человека. Согласно его подсчетам, голова- 1/7 роста, кисть руки, лицо- 1/10, ступня -1/6. Однако образ, описанный греком, имел достаточно крупные и квадратные черты, вместе с тем данные каноны стали своеобразной нормой для античного периода и основой для художников эпохи ренессанса. Поликлерт воплотил же свой образ в статуе Дорифор, в которой соотношение частей тела показывает мощь физической силы. Плечи широкие, практические такие же, как и высота туловища, ½ высоты тела – лонное сращение, а размер головы 8 раз можно уложить по высоте тела.

Автор золотого правила, Пифагор, считал идеальным то тело, в котором промежуток от

темени до пояса относился к общей длине 1:3. Напомним, что согласно правилу золотого сечения, пропорциональное соотношение, где целое относится к своей большей части, так же как и большая к меньшей. Данное правило использовали, создавая идеальные пропорции, такие мастера как Мирон, Пракситель и другие. Данные соотношения были соблюдены и при воплощении шедевра «Афродита Милосская», созданного Агесандром.

Уже не одно тысячелетие ученые ищут математические взаимосвязи в пропорциях человека и достаточно долгое время основой всех измерений были отдельные части тела, например локоть, ладони… Изучая идеальные пропорции, учеными было установлено, что размеры тела у женщин и мужчин отличаются, однако отношение частей тела друг к другу равняются примерно одинаковым числам. Так, в середине 20 века ученый из Англии — Эдинвург за основу канона человеческого тела взял музыкальный аккорд. Идеальные пропорции мужского тела соответствовали мажорному аккорду, а женского – минору.

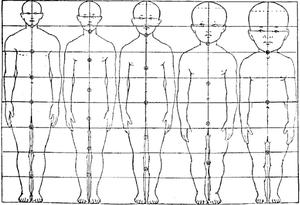
Любопытным является и тот факт, что пуп новорожденного делит его тело на две равные части. И уже затем, по мере роста, пропорции тела достигают своего апогея в развитии, которое отвечает правилу золотой пропорции.

В конце 20 века (в 90-е годы), профессор психологии Д. Сингх в результате долгих исследований нашел своеобразную формулу красоты. Согласно его мнению, идеальные пропорции женского тела представляют собой соотношение объема талии и бедер от 0,60 до 0,72. Он доказал, что для красоты важно не наличие жировых отложений, а то как они распределены по всей фигуре.

Таким образом, в зависимости от времени, эпохи и культуры идеальные пропорции тела были представлены разными показателями. Поэтому вопрос о том, существует ли идеальная фигура, остается открытым.

§5 Пропорции. Основы рисунка для учащихся 5-8 классов

Мы признаем определенные пропорциональные отношения в построении фигуры человека, его окружения, архитектуры, как нечто должное. Эмоциональное начало художественного творчества проверяется точной наукой. Выдающиеся мастера былых эпох постоянно стремились проверить алгеброй гармонию, впрочем, математика античности, средневековья и Возрождения была лишена сухости и абстрактности.

Когда мы знакомимся с историей искусства, любуемся совершенными произведениями, например античной статуей или храмом, картинами Леонардо да Винчи, Рафаэля, Энгра, то нас поражает удивительная гармония, присущая им, которая во многом определяется таким эстетическим качеством, как пропорциональность целого и деталей. Слово «пропорция» в переводе с латыни обозначает «соотношение», «соразмерность». Сравнивая предметы, окружающие нас, по величине, высоте, ширине, объему мы можем сказать, что одни из них длинные, а другие короткие, высокие и низкие, широкие и узкие, большие и маленькие и т. д. Устанавливая соотношение между предметами и между частями формы отдельного предмета, мы выясняем их пропорциональные характеристики.

Пропорциями называются размерные соотношения элементов или частей формы между собой, а также между различными объектами.

75. Измерение высоты (а) и ширины (б)

Проверять пропорции можно с помощью обычного карандаша или кисточки, при этом держать их следует на вытянутой руке.

76. Определение пропорций

Для удобства определения пропорций методом визирования можно прищурить один глаз. С помощью длины карандаша уточняют также степень наклона всей формы.

Пропорция – это гармонизация формы художественного произведения, пропорциональность – ее эстетическое качество. Соразмерность частей образует красоту формы. В основе определения пропорций лежит метод сравнения. Все эти свойства лежат и в основе грамотного рисунка. В художественной практике существует известный метод определения пропорций, называемый визированием.

Однако никакие механические способы определения пропорций не могут заменить развитого глазомера. Именно эту способность необходимо развивать в себе тренировкой.

Рисуя, нужно помнить, что мы изображаем предметы несколько меньшими их натуральной величины, поэтому необходимо придерживаться единого масштаба для определения пропорций всех объектов изображения, составляющих композицию. Таким образом, выдержать пропорции в рисунке – значит добиться соотношения величин всех частей предмета к целому в пределах выбранного формата листа.

Поиск пропорций в изображении фигуры человека является сложной задачей. Обратимся к истории, посмотрев, как решали ее художники разных эпох и разных культур.

77. Композиция пропорций человека в Древнем Египте

Единицей измерения фигуры у древнеегипетских художников служила длина среднего пальца руки, вытянутой вдоль бедра.

В Древнем Египте для изображения человеческой фигуры был разработан специальный канон – то есть такая система пропорций человеческой фигуры, которая делила изображение на части и позволяла по части определить целое и по одной части тела определить другую. Известно, что египтяне положили в основу деления фигуры 21 1/4 части. В это число входили 19 равных частей разделения самой фигуры, а 2 1/4 части приходились на изображение традиционного головного убора (ил. 77), Египтяне пользовались и специальными сетками-таблицами, которые наносили на поверхность каменной плиты или стены для создания рельефа или росписи (ил. 34а).

На сохранившихся и дошедших до нас памятниках можно видеть, что горизонтальные и вертикальные линии делят рисунок в определенных местах, что соответствует членению фигур на части. Были установлены также определенные размеры для изображения сидящих фигур и изображения разных богов в соответствии с их иерархическим старшинством (одни должны быть выше, другие немного ниже). Детей изображали как взрослых, но значительно меньшими по размеру. Художнику необходимо было знать установленные каноном нормы и научиться вписывать в них изображения, пользуясь сеткой-таблицей. Единая система обучения и строгое соблюдение выработанных норм позволяли выполнять части одного произведения разными мастерами. Когда такие части составляли в единую композицию, то они точно сходились и не было нарушения пропорций.

Вся история учения о пропорциях связана с поисками законов гармонии и красоты. В Древней Греции систему идеальных пропорций человеческой фигуры создал скульптор Поликлет в V веке до н. э. Его теоретическое сочинение на эту тему называлось «Канон», а выражением в скульптуре этой системы явилась его статуя «Дорифор», что означает копьеносец. Мастер изобразил атлета-юношу, победителя в соревнованиях по метанию копья, в момент, когда после одержанной победы он совершает круг почета по стадиону и его приветствуют восторженные зрители.

Открытие пропорций, полагают, принадлежит к заслугам древневосточной математики, античная же традиция связывает его с именем выдающегося философа и математика Пифагора, жившего в VI веке до н. э. Универсальный принцип гармонии и красоты в пропорциях получил название «золотое сечение», которое олицетворяло равновесие знания, чувств и силы. Золотое сечение возникает при делении отрезка на две неравные части таким образом, при котором весь отрезок относится к большей его части, как большая к меньшей (0,618).

78. ПОЛИКЛЕТ. Дорифор

Поликлет создал новые членения пропорций человеческой фигуры, однако точных сведений о том, что именно было выбрано за единицу меры – величина ладони, ступни или высота головы,- не сохранилось.

79. С. БОТТИЧЕЛЛИ. Канон пропорций

80. МИКЕЛАНДЖЕЛО. Пропорции фигуры человека

Знакомство с золотым сечением сыграло немалую роль в работе античных архитекторов, скульпторов и живописцев. Обучающимся рисунку будет интересно узнать правило, наглядно прослеживающееся в древнегреческих статуях: при делении туловища человека в соответствии с золотым сечением легко найти уровень пупа и локтя, при повторном делении двух отрезков в противоположных направлениях определяется высота колена и нижний уровень шеи.

Примерами использования золотого сечения может быть античная голова Афродиты и любое из произведений художника Рафаэля. В поисках гармонии художники интуитивно всегда следовали этому принципу и в той или иной мере приближались к идеальным соотношениям, но теоретически принцип золотого сечения был сформулирован в эпоху Возрождения. Леонардо да Винчи, изучавший и глубоко анализировавший опыт древних, разрабатывая правила изображения человеческой фигуры, пытался на основе литературных сведений восстановить так называемый «квадрат древних». Он выполнил рисунок, в котором показана пропорциональная закономерность в соотношении частей тела человека.

Над выработкой канонов пропорций трудились такие знаменитые мастера эпохи Возрождения, как С. Боттичелли и Микеланджело. Проблема поиска системы идеальных пропорций остается актуальной и для художников и архитекторов XX века. Французский зодчий Jle Корбюзье в 1947 году разработал «Модулор» – систему деления человеческой фигуры на согласованные в золотом сечении отрезки от ступни до талии, от талии до затылка и от затылка до верха пальцев поднятой руки. На этой основе была создана школа модулей для архитектурного проектирования и дизайна.

Античное искусство установило идеальные пропорции и для головы человека, согласно которым она по вертикали от темени до конца подбородка делится на две равные части линией глазных впадин (ил. 83). Каждую из этих половин можно, в свою очередь, разделить на две равные части: верхнюю – линией волос, а нижнюю – основанием носа. Получается четыре равные части. Расстояние между глазами принимается равным ширине крыльев носа.

81. ЛЕОНАРДО ДА ВИНЧИ. «Квадрат древних»

82. ЛЕ КОРБЮЗЬЕ. Модулор

Расстояние от бровей до основания носа определяет величину ушей. В действительности редко встречаются у людей такие идеальные пропорции, но знать их необходимо, чтобы видеть отклонения от нормы и лучше понимать индивидуальные пропорции живой натуры.

Пока общая форма головы не решена, не найдены ее пропорции, нельзя переходить к отделке деталей. Портретное сходство зависит во многом от правильно выдержанных общих пропорций.

Следует помнить, что при определении пропорций лучше сравнивать отношения нескольких деталей на рисунке с соотношениями таких же деталей в натуре.

Переходя к эмоциональной характеристике портретируемого, полезно изучить схемы лица при различных психологических состояниях на ил. 84.

83. Пропорции головы

84. Схематическая таблица сокращения мускулов лица при различных психологических состояниях (по М. Дювалю): 1 – спокойствие, 2 – печаль, 3 – радость, 4 – боль, 5 – смех, 6 – плач, 7 – презрение, 8 – внимание, 9 – размышление

Посмотрите, как с помощью самых простых средств, всего лишь опуская или приподнимая уголки губ, брови или веки, можно передать печаль, радость, боль, смех, презрение, внимание и т. д. (ил. 84-85).

85. Лица в различном эмоциональном состоянии

Поделитесь на страничке

Следующая глава >

Правильные пропорции человека – путь от гармонии к долгожительству

Многие художники и ученые не один год пытались разгадать тайны человеческого тела, искали совершенные пропорции человека. Этот вопрос и сегодня остается открытым, так как на подсознательном уровне каждый из нас стремится к гармонии и совершенству.

Идеальные пропорции человека

Ответ на этот сложный вопрос очень прост. В первую очередь идеальные пропорции человека должны гармонировать с учетом его телосложения, роста и возраста.

Если внимательно осмотреть свое тело, можно заметить, что расстояние от запястья до начала локтевого сгиба равно размеру стопы. Длина голени (включая стопу) будет равна длине бедра, а коленная чашечка будет делить ногу на две совершенно равные доли.

Бедренная кость при этом однозначно длиннее голени, а она длиннее стопы. Также предплечье короче плечевой кости, но длиннее кисти. Опущенная вниз рука достанет кончиками пальцев точно до половины бедра.

За единицу измерения тела человека обычно принимают длину головы. Идеальные параметры соотношения длины головы и высоты тела человека составляют 1/8 и 1/7,5 у мужчин и женщин соответственно. В последнее время происходит тенденция изменения пропорций тела, и на сегодняшний день соотношение 1:9 для человека считается нормой.

Идеальные пропорции лица человека

Лицо человека, как и его тело, должно иметь строгие пропорциональные соотношения:

— расстояние от границы волос до начала подбородка должно составлять 1/10 часть роста человека;

— длина от макушки до начала подбородка должна составлять 1/8 часть роста человека;

— расстояние от начала подбородка до кончика носа равно 1/3 части длины всего лица;

— расстояние от границы волос до линии бровей должно составлять 1/3 часть длины лица;

— длина ушей равна 1/3 части общей длины лица.

Такую закономерность можно проследить на лице каждого человека. Но в жизни люди с идеальными пропорциями лица встречаются достаточно редко. В результате некоторых отклонений от совершенных пропорций и возникают индивидуальные черты лица. Именно поэтому все люди разные.

Изменение пропорции человека с возрастом

С возрастом пропорции тела меняются. Дети заметно отличаются от взрослых длинным туловищем, короткими ногами и большой головой. Так, у новорожденного длина головы равна 1/4 части его роста, в два года – 1/5 части, в шесть лет – 1/6 части, а у взрослого человека – уже 1/8 части. Как видно, только по мере взросления пропорции ребенка начинают соответствовать взрослому человеку.

Основные типы телосложения

Зная размеры тела, можно рассчитать тип телосложения человека. Расчет довольно прост и производится с помощью значения индекса ИП (Пинье).

Для расчета индекса Пинье необходимо просуммировать массу тела и окружность грудной клетки. Далее из значения длины тела нужно вычесть полученный выше результат.

Если индекс Пинье равен 30 и больше, то человек относится к астеническому типу и у него худощавое телосложение.

Если же индекс равен значению до 30, то человека можно отнести к атлетическому типу с нормальным телосложением.

Если же данный индекс менее 10, то человек относится к пикническому типу с тучным телосложением.

Результаты исследований

В результате многочисленных исследований было доказано, что пропорции тела человека непосредственно влияют на продолжительность его жизни. Этот факт аргументировали ученые из Великобритании совместно с немецким Институтом здорового питания. Специалисты проводили исследования взаимосвязи риска преждевременной смерти с пропорциями тела и пришли к единогласному выводу, что при большом обхвате талии повышается вероятность преждевременной смерти.

Заключение

Практически все части тела человека имеют определенные пропорциональные соотношения, но их значения могут иметь индивидуальные отклонения. Если же ваши пропорции не совпадают с идеальными параметрами, не огорчайтесь. Ведь главными качествами в человеке являются его индивидуальность, гармония и здоровье!

Образ человека в древнегреческой и римской культуре (стр. 3 из 5)

Главной задачей искусства V в. до н.э. было правдивое изображение человека, сильного, энергичного, полного достоинства и равновесия душевных сил — победителя в персидских войнах, свободного гражданина полиса, в котором нравственная красота неотделима от физической. И в этом смысле искусство греков V-IV в. до н.э. справедливо стали называть классикой, оно явилось образцом для подражания.

В искусстве в полной мере воплотился идеал человека-героя, совершенного физически и нравственно. Большинство скульптур дошли до нас в поздних римских копиях. Из сохранившихся греческих оригиналов есть знаменитая статуя «Дельфийского возничего», созданная около 470 г. до н.э. Молодой человек изображен в рост в длинном хитоне, перехваченном поясом на талии, с вожжами в руках. Струящиеся складки его одежды напоминают каннелюры дорической колонны, лицо полно сдержанной силы, спокойствия, торжественности и благородства, линии лба, носа, бровей и губ безупречны по рисунку. Идеально прекрасный образ не лишен, однако, жизненности. В зрачки глаз были вставлены цветные камни, в результате его лицо обретает необычайную живость, одухотворенность. Этот образ, полный гармонии, олицетворяет идеал совершенного человека, равного героям эпоса [9].

В это время достигает расцвета реалистическая скульптура, выполнявшаяся в основном из мрамора, который, как и в архаическую эпоху, раскрашивали, и бронзы. Монументальность, стремление к гармонии, пропорциональности, созданию идеальных образов богов и людей отличают творчество великих скульпторов V в. до н.э.: Фидия (середина V в. до н. э) — статуи «Афина — воительница», «Афина-Парфеносо для Парфенона в Афинах, «Зевс» — для храма в Олимпии; Мирона (V в. до н. э) — знаменитый «Дискобол», Поликлета (2-я пол. V в. до н. э) — статуя «Гера», выполненная из золота и слоновой кости, «Дорифор» «Копьеносец», «Раненая амазонка». (Скульптура Поликлета «Дорифор» настолько поразила современников гармонней пропорций, что была признана каноном идеального телосложения). В сохранившихся фрагментах сочинения «Канон» Поликлет вывел цифровой закон идеальных пропорциональных соотношений человеческого тела [8].

Наиболее известен среди работ Мирона из Элевтер «Дискобол» (около 460-450 гг. до н. э), изображающий атлета в момент наивысшего напряжения перед броском диска. Его рука отведена назад, еще момент — и юноша пустит снаряд далеко вперед. Мирон, которого волновала проблема изображения движения, улавливает тот момент, который лежит между замахиванием и самим броском. Это переходное состояние позволяет скульптору не запечатлевать какое-то определенное движение атлета, а передать всю мощь внутреннего напряжения, необходимого для победы [9]. Физическое, а значит, и внутреннее совершенство этих статуй утверждает мысль о человеке как о мериле всего сущего.

Смерть Фидия (431 г. до н.э.) и затем Перикла совпала с концом высокой классики, эстетический идеал которой выражен в словах Перикла: «Мы любим прекрасное, соединенное с простотою, и мудрость без изнеженности».

Эпоха кризиса полиса. Первые признаки кризиса полиса проявились уже в годы Пелопоннесской войны (431-404 до н.э.) между Афинами и Спартой за господство в Греции.

Кризис полисной идеологии оказал большое влияние на развитие греческой скульптуры. Восхищение доблестями прекрасного и благородного гражданина, которого изображали мастера V в. до н.э., сменилось интересом к человеческой личности. В скульптуре на смену мужественности и суровости образов строгой классики приходит интерес к душевному миру человека, и в пластике находит отражение более сложная и менее прямолинейная его характеристика.

Наиболее прославленные скульпторы IV в. до н.э. — Пракситель (2-я треть IV в. до н.э.), Скопас (W в. до н.э.), Лисина (2-я пол. IV в. до н.э.). Изображая богов, воплощающих идеальную красоту, Пракситель насыщает их чисто человеческими настроениями самых различных оттенков («Афродита Книдская», Аполлон, убивающий ящерицу», «Отдыхающий Гермес» и др.). Так, в единственной дошедшей до нас в подлиннике скульптора Праксителя мраморной статуе Гермеса (покровителя торговли и путешественников, а также вестника, «курьера» богов; статуя исполнена около 330 г. до н.э. и была найдена в ХIX в. в Олимпии) мастер изобразил прекрасного юношу, небрежно облокотившегося на пень, в состоянии покоя и безмятежности. Задумчиво и нежно он глядит на младенца Диониса, которого держит на руках. На смену мужественной красоте атлета V в. до н.э. приходит красота несколько женственная, изящная, но и более одухотворенная. Особой славой пользовалась другая скульптура Праксителя — статуя Афродиты Книдской. Это было первое в греческом искусстве изображение обнаженной женской фигуры. Статуя стояла на берегу полуострова Книд, и современники писали о настоящих паломничествах сюда, чтобы полюбоваться красотой богини, готовящейся войти в воду и сбросившей одежды на стоящую рядом вазу.

В отличие от Праксителя, изображающего легкие, приятные человеку эмоции, Скопас продолжил традиции высокой классики, создавая образы монументально-героические. Но от образов V в. их отличает драматическое напряжение всех духовных сил («Геракл», «Вакханка» и др.) [4].

Переосмыслив канон изображения человека, созданный в V в. до н.э. Поликлетом, Лисипп делал тела людей с более легкими, удлиненными пропорциями. Он стремился создавать жизненно достоверные статуи. Лисипп стремился их сделать более жизненными, не идеально совершенными, а характерно-выразительными. В портретных бюстах Сократа, Александра Македонского он выразил сложную внутреннюю жизнь человека [8].

В эпоху эллинизма (III в. до н.э. и последние десятилетия I в. до н. э) искусство характеризуется исключительно интенсивным развитием всех художественных форм, связанных и с греческими, и с «варварскими» принципами культуры, с развитием науки, техники, философии, религии, с расширением кругозора. Это объясняется и обширными военными походами, и торговыми контактами, и научными путешествиями того времени. Границы, на которых существовал гражданин полиса, и которые формировали его мировоззрение, снимаются, и возникает неведомое ранее «чувство мировых просторов». Этот сложный мир, лишенный привычной гармония, был новым. Его необходимо было понять, а значит, и выразить в художественных формах средствами искусства.

В эпоху эллинизма продолжают развиваться тенденции, наметившиеся в греческой скульптуре IV в. до н.э. Проявляется повышенный интерес к личности, ее эмоциям, характерные черты скульптуры этого времени — динамичность, выразительность. Активно развивается жанровое направление, появляются новые школы — в Пергаме, на Родосе, в Александрии. В этот период были созданы всемирно известные рельефы пергамского алтаря Зевса, скульптуры «Афродита Мелосская», «Ника Самофракийская», скульптурные группы «Лаокоон», «Фарнезский бык», скульптурный портрет Демосфена. Одним из семи чудес света считался не дошедший до нас Родосский Колосс — бронзовая статуя бога солнца Гелиоса, достигавшая в высоту 37 м.

На острове Самофракия была поставлена статуя богини победы Нике в честь победы родосского флота над врагами. Воздвигнутая на пьедестале, напоминающем нос корабля, фигура Нике органически вписывалась в ландшафт со скалой, обрывающейся в море. Развевающийся хитон, мощные отведенные назад крылья, могучее тело, устремленное вперед, придают ей нечто титаническое, неудержимо стремительное, страстное, создают победный, ликующий, торжественный образ.

Нередко скульпторы обращались и к классическим образцам. Примером этого может служить статуя Афродиты с острова Мелос (скульптор Агесандр; 120 г. до н. э), известная более в римском названии как Венера Милосская. В многочисленных изображениях Афродиты, созданных в эллинистическую эпоху, всегда подчеркивалось только чувственное начало. Образ же Афродиты с острова Мелос полон высокой нравственной силы, что говорит о глубоком понимании мастером идеалов высокой классики.

Большой шаг вперед делает эллинистический скульптурный портрет, в котором вполне отчетливо стремление не столько к передаче характерных особенностей внешнего облика модели, сколько к воплощению духовного мира (например, портреты Аристотеля и Менандра).

Искусство эпохи эллинизма более демократично, лишено жестких норм, канонов, более реалистично и гуманистично, ибо человек с его страстями и в реальном обличье стал центром внимания искусства того периода. Полноправным в скульптуре стало бытовое направление, иногда натуралистического толка, характерного, например, для александрийской школы («Старик, вынимающий занозу из ноги»), иногда более лирическое, поэтичное, как, например, терракотовые статуэтки из Танагры. На смену идеалам высокой гражданственности эллинизм принес иные решения: замечательные по наблюдательности изображения детского тела («Мальчик с гусем», скульптор Боэф), сложные образы декоративной скульптуры, связанной с расцветом паркового искусства и строительством загородных вилл (изображение Нила с шестнадцатью детскими фигурками — аллегориями 16 локтей, на которые река поднимается во время разлива, неизвестный мастер) [4].

Древнегреческая литература — древнейшая из европейских литератур, у истоков которой (VIII в. до н.э. находятся «Илиада» и «Одиссея», приписываемые слепому певцу Гомеру. Литература — еще один росток духовной культуры, выросший из мифологии.

Эллинам первым удалось с помощью поэтического мышления, художественных средств объяснить природу и человека, показать их в многообразии и развитии. Древнегреческая литература полна разнообразных сюжетов о борьбе богов и героев со злом, несправедливостью, стремления к достижению гармонии в жизни. В ней рождается идея единства внешней и внутренней красоты, физического и духовного совершенства личности. Человек смертен, но бессмертна слава героев [10].

Исследовательская работа «Золотое сечение в пропорциях тела человека»

ВВЕДЕНИЕ

Эталонами красоты человеческого тела, образцами гармонического телосложения издавна считаются великие творения греческих скульпторов: Фидия, Поликтета, Мирона, Праксителя. Можно ли выразить красоту человека с помощью формул и уравнений? Математика дает утвердительный ответ. В создании своих творений греческие мастера использовали принцип золотой пропорции. Золотое сечение является мерилом гармонии в природе и в произведениях искусства на протяжении многих веков. Его изучением занимались люди античности и эпохи Возрождения. В ХIХ и ХХ веке интерес к золотому сечению возродился с новой силой.

Соответствуют ли современные люди тем идеальным пропорциям строения человеческого тела, которые дошли до нас с античных времен? На этот вопрос мы постараемся ответить в исследовательской работе «Золотое сечение в пропорциях тела человека».

Цель работы: изучение золотого сечения, как идеальной пропорции строения человеческого тела.

Задачи:

1. изучить литературу по теме исследовательской работы;

2. дать определение золотому сечению, познакомиться с его построением, применением и историей;

3. узнать математические закономерности в пропорциях тела человека;

4. научиться находить золотое сечение в пропорциях людей;

5. определить соответствие пропорций человеческого тела золотому сечению.

Гипотеза: пропорции каждого человеческого тела соответствуют золотому сечению.

Объект исследования: человек.

Предмет исследования: золотое сечение в пропорциях человеческого тела.

Методы исследования: измерение роста и частей тела человека, обработка полученных результатов математическими методами с помощью программы Microsoft Office Excel 2007, сравнительный анализ полученных измерений со значением золотого сечения.

Глава 1 Золотое сечение

1. 1. Понятие золотого сечения

Пифагор показал, что отрезок единичной длины АВ (рисунок 1.1). можно разделить на две части так, что отношение большей части (АС=х) к меньшей (СВ=1-х) будет равняться отношению всего отрезка (АВ=1) к большей части(АС=х):

Рисунок 1.1 – Деление отрезка в крайнем и среднем отношении

По свойству пропорции .. х²=1-х,

х²+х-1=0. (1)

Положительным корнем этого уравнения является , так что отношения в приведенной пропорции равны: =≈1,61803 каждое.

Такое деление (точкой С) Пифагор называл золотым делением, или золотой пропорцией, Евклид – делением в крайнем и среднем отношении, а Леонардо да Винчи – общепринятым сейчас термином «золотое сечение».[7,с.18-19]

Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему. [2,с.8]

Величину золотого сечения принято обозначать буквой Ф. Это сделано в честь Фидия- творца бессмертных скульптурных произведений. [1, с.141]

Ф=1,618033988749894. Это значение золотого сечения с 15 знаками после запятой. Более точное значение Ф можно увидеть в Приложении А.

Так как решение уравнения (1) является отношением между длинами частей отрезка, оно не зависит от длины самого отрезка. Другими словами, значение золотого сечения не зависит от первоначальной длины. [4, с.24,25]

1.2 Построение и применение золотого сечения

Рассмотрим геометрическое построение золотого сечения (рисунок 1.2) с помощью прямоугольного треугольника АСВ, в котором стороны АВ и АС имеют следующие длины: АВ = 1, АС = 1/2. Проведем из центра окружности С дугу через точку А до пересечения с отрезком СВ, получим точку D . Затем проведем через точку D дугу с центром окружности В до пересечения с отрезком АВ. Получили искомую точку Е, делящую отрезок АВ в золотой пропорции. [5, с.12]

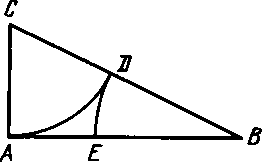
Рисунок 1.2 – Геометрическое построение золотого сечения

Еще Пифагор и пифагорейцы использовали золотое сечение для построения некоторых правильных многогранников — тетраэдра, куба, октаэдра, додекаэдра, икосаэдра.

Евклид в III в. до н. э. использует вслед за пифагорейцами золотую пропорцию в своих «Началах» для построения правильных (золотых) пятиугольников, диагонали которых образуют пентаграмму. [7, с.19]

В пентаграмме на рисунке 1.3 точки пересечения диагоналей делят их в золотом сечении, т. е. АВ/СВ = CB/DB = DB/CD .

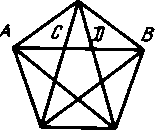
Рисунок 1.3 — Пентаграмма

Арифметически отрезки золотой пропорции выражаются бесконечной иррациональной дробью. АС=0,618…, СВ=0,382…. В практике применяется округление: 0,62 и 0,38. Если отрезок АВ принять за 100 частей (рисунок 1.4), то большая часть отрезка равна 62, а меньшая – 38 частям. [2, с.10]

Этот способ построения золотого сечения используют художники. Если высоту или ширину картины разделить на 100 частей, то больший отрезок золотой пропорции равен 62, а меньший – 38 частям. Эти три величины позволяют нам построить ряд отрезков золотой пропорции. 100, 62, 38, 24, 14, 10 – это ряд величин золотой пропорции, выраженных арифметически. [2, с.11]

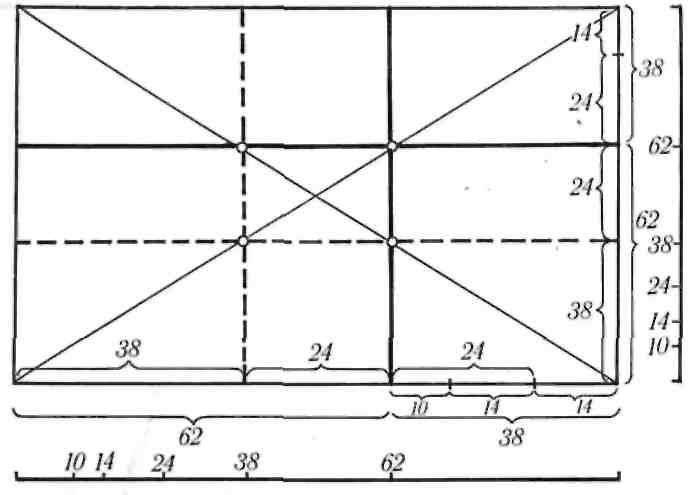
Рисунок 1.4 — Линии золотого сечения и диагонали на картине

Пропорции золотого сечения часто использовались художниками не только при проведении линии горизонта, но и в соотношениях между другими элементами картины.

Леонардо да Винчи и Альбрехт Дюрер находил золотое сечение в пропорциях человеческого тела. Древнегреческий скульптор Фидий использовал его не только в своих статуях, но и при оформлении храма Парфенона.[8, с.99-100] Страдивари использовал это соотношение при изготовлении своих знаменитых скрипок. [2, с.7]

Форма, организованная при помощи пропорций золотого сечения, вызывает впечатление красоты, приятности, согласованности, соразмерности, гармоничности. [2, с.6]

Учение о золотом сечении получило широкое применение в математике, физике, химии, живописи, эстетике, биологии, музыке, технике.

1.3 История золотого сечения

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Однако еще задолго до рождения Пифагора древние египтяне и вавилоняне использовали принципы золотого сечения в архитектуре и искусстве. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

Платон (427…347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления. [3, с17,18]

Античные скульпторы и архитекторы широко использовали число 1,62 или близкие к нему числовые соотношения в своих художественных произведениях. Например, в фасаде древнегреческого храма Парфенона присутствуют золотые пропорции.

В дошедшей до нас античной литературе золотая пропорция впервые упоминается в «Началах» Евклида (325…265 гг. до н.э.) во второй книге, а в шестой книге дается определение и построение деления отрезка в крайнем и среднем отношении. [4,с.148]

В эпоху итальянского Возрождения возникает новая волна увлечения золотым сечением. Золотая пропорция возводится в ранг главного эстетического принципа. Леонардо да Винчи именует ее «Sectio autea», откуда и происходит сам термин «золотое сечение» или «золотое число». Лука Пачиоли в 1509 г. пишет первое сочинение о золотой пропорции, озаглавленное «De divina Proportioned», что значит «О божественной пропорции». Иоганн Кеплер, первым упоминающий о значении этой пропорции в ботанике, говорит о ней, как о «бесценном сокровище, как об одном из двух сокровищ геометрии» и называет ее «Sectio divina» (божественное сечение). Нидерландский композитор Якоб Обрехт (1430—1505 гг.) широко использует золотое сечение в своих музыкальных композициях, которые уподобляют «кафедральному собору, созданному гениальным архитектором».

После эпохи Возрождения почти на два столетия золотое сечение было предано забвению. В середине XIX в. немецкий ученый Цейзинг делает попытку сформулировать всеобщий закон пропорциональности и при этом вновь открывает золотое сечение. В своих «Эстетических исследованиях» (1855) он показывает, что этот закон проявляется в пропорциях человеческого тела (рисунок 1.5) и в теле тех животных, формы которых отличаются изяществом. В теле античных статуй и хорошо сложенных людей пуп является точкой деления высоты тела в золотом сечении. [5, c.4]

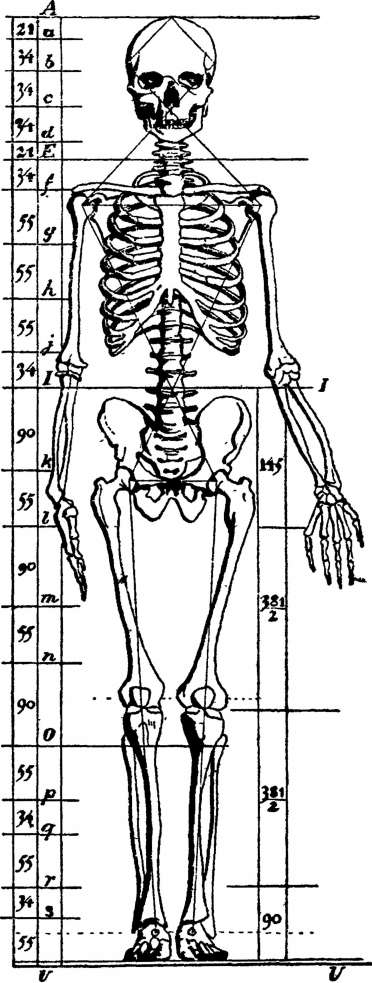
Рисунок 1.5 – Числовые отношения в человеческом теле (по Цейзингу)[6,c.59]

Пропорциональные отношения, близкие к золотому сечению, Цейзинг находит в некоторых храмах (в частности, в Парфеноне), в конфигурациях минералов, растений, в звуковых аккордах музыки.

В конце XIX в. немецкий психолог Фехнер проводит ряд психологических опытов для выяснения эстетического впечатления от прямоугольников, имеющих различные отношения сторон. Опыты оказались чрезвычайно благоприятными для золотого сечения.

В XX в. интерес к золотому сечению возрождается с новой силой. В первой половине века композитор Л.Сабанеев формулирует общий закон ритмического равновесия и при этом обосновывает золотое сечение в качестве некоторой нормы творчества, нормы эстетической конструкции музыкального произведения. О значении золотого сечения в природе и искусстве пишут Г. Е. Тимердинг, М. Гика , Г. Д. Гримм.

К «задаче о кроликах», с которой связано возникновение чисел Фибоначчи, в своих истоках восходит математическая теория биологических популяций. Закономерности, описываемые числами Фибоначчи и золотой пропорцией, обнаруживают во многих явлениях физического и биологического мира («магические» ядра в физике, ритмы мозга и др.).

Советский математик Ю. В. Матиясевич с использованием чисел Фибоначчи решает 10-ю проблему Гильберта. Академик Г.В.Церетели обнаруживает золотое сечение в поэме Шота Руставели «Витязь в тигровой шкуре». Возникают изящные методы решения задач теории поиска и теории программирования, основанные на числах Фибоначчи и золотой пропорции.

В последние десятилетия числа Фибоначчи и золотая пропорция неожиданно проявили себя в основании цифровой техники

Во второй половине XX века к числам Фибоначчи и золотому сечению обращаются представители практически всех наук и искусств (математики, физики, химии, ботаники, биологии, психологии, поэзии, архитектуры, живописи, музыки) [5, с.4,5], потому что золотое сечение – ключ к пониманию секретов совершенства в природе и искусстве.

Глава 2 Идеальные пропорции человеческого тела

Уже тысячелетия пытаются люди найти математические закономерности в пропорциях тела человека, прежде всего человека хорошо сложенного, гармоничного.

Древние греки, считавшие золотое сечение проявлением гармонии в природе, создавали статуи людей с соблюдением правила золотого сечения. В XIX веке профессор Цейзинг подтвердил это, измерив сохранившиеся до наших дней древнегреческие статуи. Цейзинг даже выделил части тела человека, которые, по его мнению, наиболее точно соответствуют золотому сечению. Если разделить тело человека согласно правилу золотого сечения, то линия пройдет в области пупка. Длина плеча относится к общей длине руки также согласно золотому сечению. Соотношение частей лица, длины фаланг пальцев руки и многие другие части тела подпадают под правило золотого сечения (рисунок 2.1). [3, с.24,25]

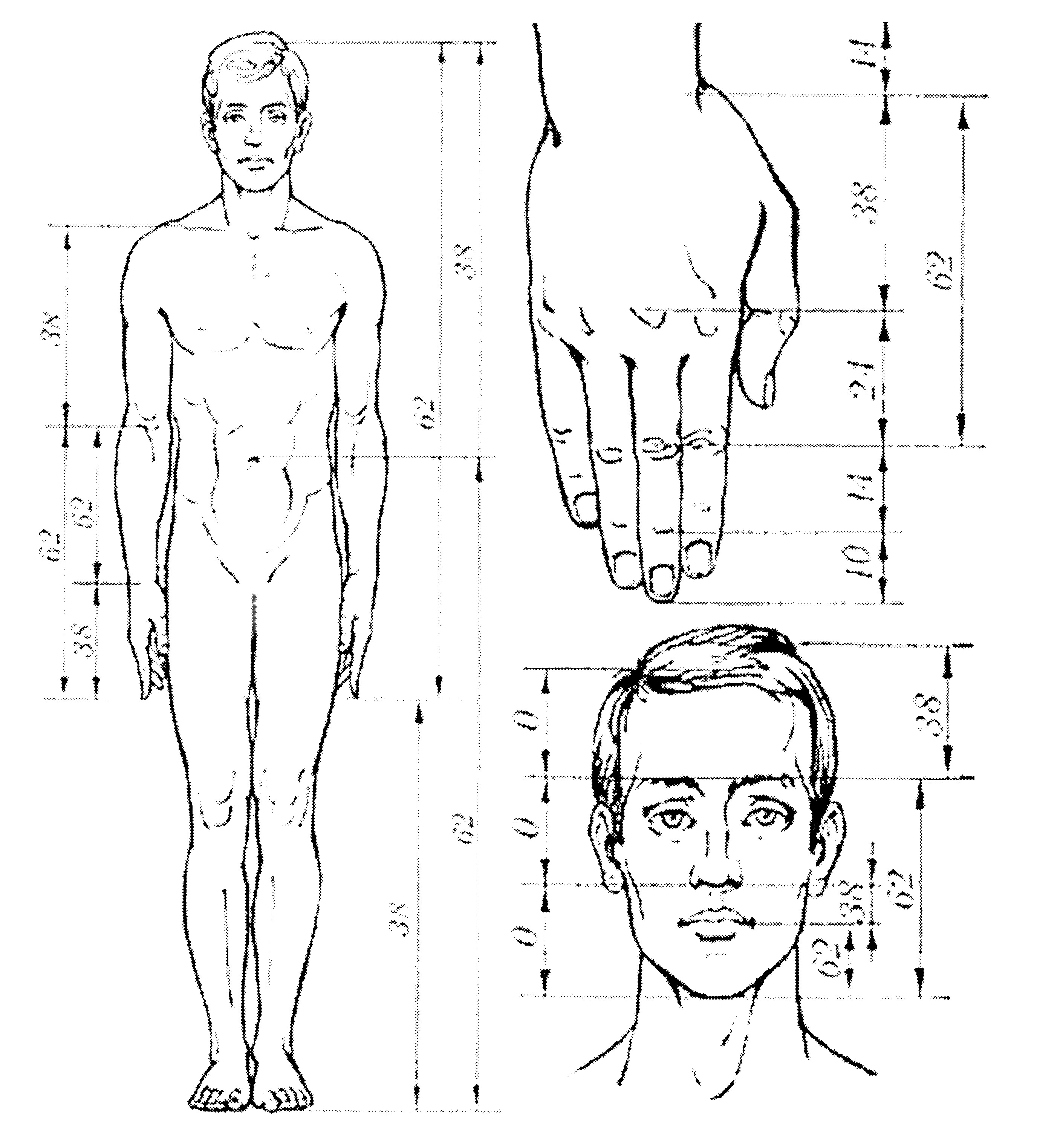
Рисунок 2.1 – Золотое сечение в строении тела человека

Золотая пропорция занимает ведущее место в художественных канонах Леонардо да Винчи и Дюрера. В соответствии с этими канонами золотая пропорция отвечает делению тела на две неравные части линией талии.

Высота лица (до корней волос) относится к вертикальному расстоянию между дугами бровей и нижней частью подбородка, как расстояние между нижней частью носа и нижней частью подбородка относится к расстоянию между углами губ и нижней частью подбородка, это отношение равно золотой пропорции.

Пальцы человека состоят из трех фаланг: основных, средних и ногтевых. Длина основных фаланг всех пальцев, кроме большого, равна сумме длин двух остальных фаланг, а длины всех фаланг каждого пальца соотносятся друг к другу по правилу золотой пропорции. [1, с.144,145]

Леонардо применил научные знания о пропорциях человеческого тела к теориям Пачоли и Витрувия о красоте. На рисунке Леонардо «Витрувианский человек» мужская фигура, вписанная в круг и квадрат (рисунок 2.2).

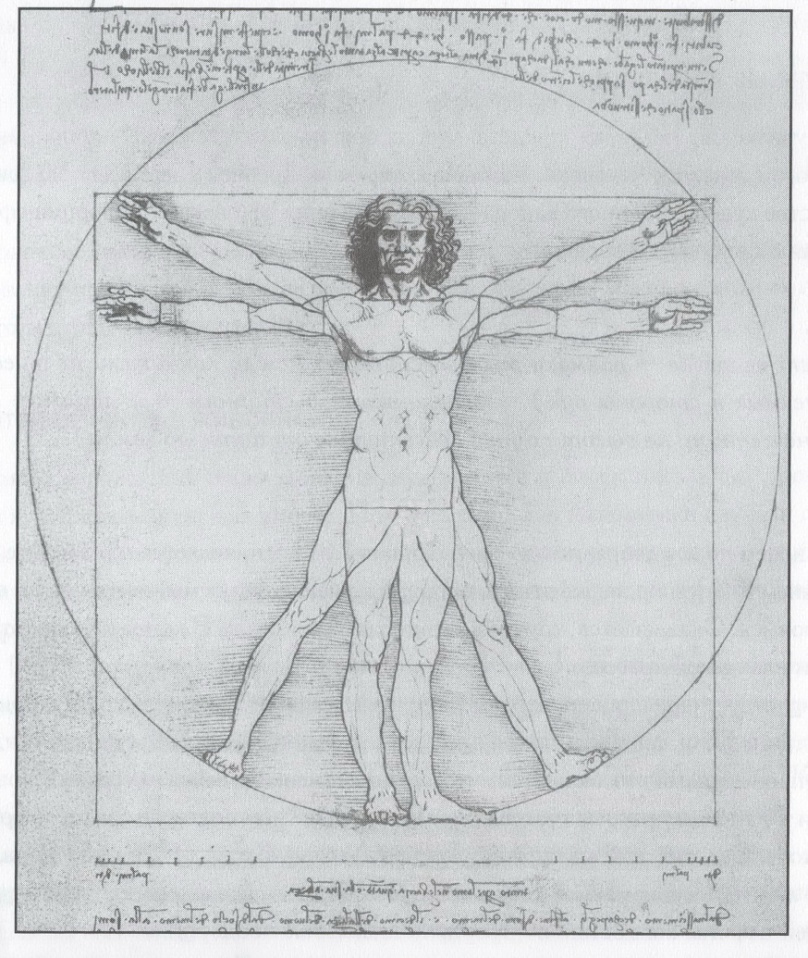
Рисунок 2.2 – «Витрувианский человек» Леонардо да Винчи

Квадрат и круг имеют разные центры. Гениталии человека являются центром квадрата, а пупок – центром круга. Идеальные пропорции человеческого тела на таком изображении соответствуют отношению между стороной квадрата и радиусом круга: золотому сечению. [4,с.100,101]

«Витрувианский человек» представляет собой приблизительные пропорции тела обычного взрослого человека, которые со времен Древней Греции использовались в качестве художественного канона для изображения человека. Пропорции сформулированы следующим образом:

Рост человека = размаху рук (расстоянию между кончиками пальцев разведенных в стороны рук) = 8 ладоням= 6 ступням= 8 лицам = 1,618 умноженному на высоту пупка (расстояние от пупка до земли).[4,с.102]

Одним из высших достижений классического греческого искусства может служить статуя «Дорифор» («Копьеносец»), изваянная Поликтетом (рисунок 2.3).

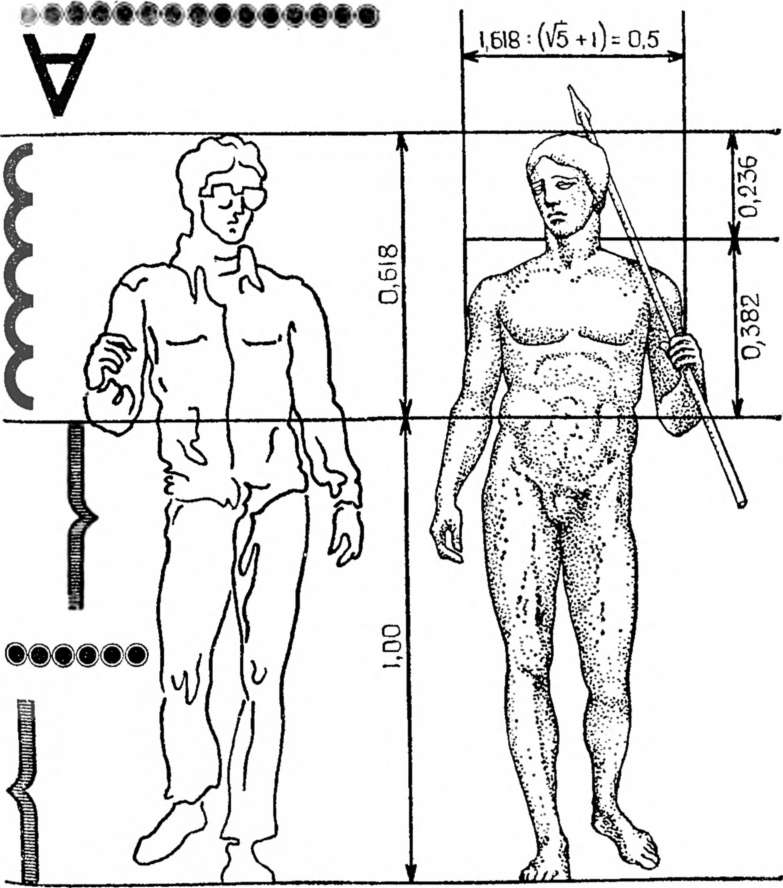
Рисунок 2.3 – Статуя «Дорифор» греческого скульптора Поликтета

Фигура юноши выражает единство прекрасного и доблестного, лежащих в основе греческих принципов искусства. Широкие плечи почти равны высоте туловища, половина высоты тела приходится на лонное сращение, высота головы восемь раз укладывается в высоте тела, а золотой пропорции отвечает положение пупка на теле атлета.[1,c.141,142]

В середине XIX века немецкий ученый Цейзинг находил, что все тело человека в целом и каждый отдельный его член связаны математически строгой системой пропорциональных отношений, среди которых золотое сечение занимает важнейшее место. Измерив тысячи человеческих тел, он установил, что золотая пропорция есть среднестатистическая величина, характерная для всех хорошо развитых тел. Средняя пропорция мужского тела близка к 13/8= 1,625, а женского — к 8/5=1,60, у новорожденного пропорция равна 2, к 13 годам она равна 1,6, а к 21 году равняется мужской (рисунок 2.4). [3, с.20]

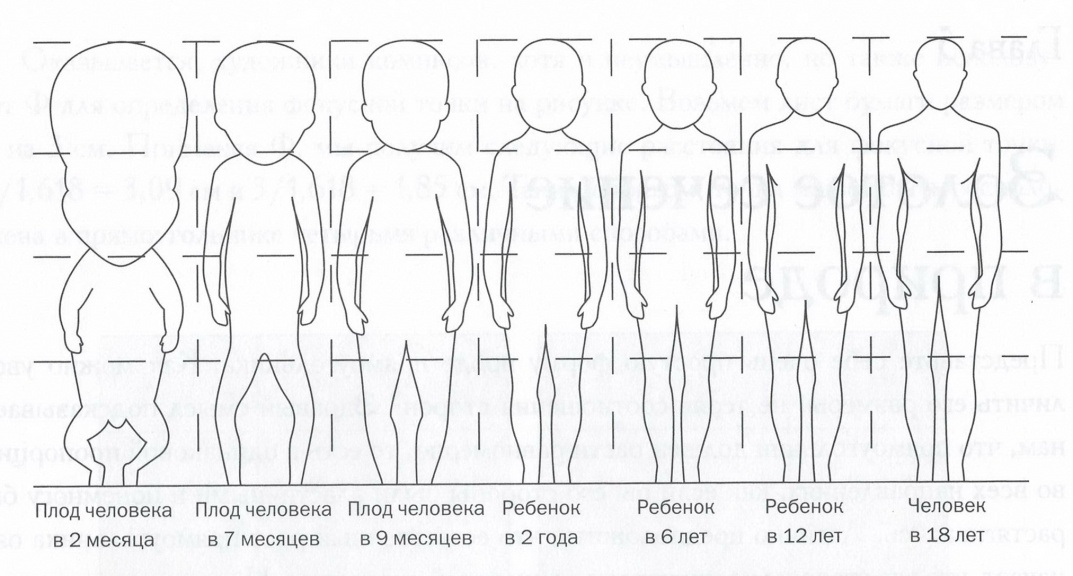
Рисунок 2.4 – Сравнение пропорций головы и тела человека на различных этапах развития [4,c.126]

Бельгийский математик Л.Кетле в XIX веке установил, что человек идеален только при подсчете среднего арифметического. В 1871г. его исследования пропорций тел жителей Европы полностью подтвердили идеальные пропорции.[4,с.102]

Золотую пропорцию можно считать некоторой «константой гармонии», идеальным пределом, к которому стремится тело человека в своем развитии.

Глава 3 Золотое сечение в пропорциях тела человека. Исследование

Мы проверяли гипотезу о том, что пропорции каждого человеческого тела соответствуют золотому сечению.

Для исследования были привлечены учащиеся 1-х, 5-х, 9-х и 11-х классов и учителя разного возраста(от 25 до 53 лет).

В теле человека пуп является точкой деления высоты тела в золотом сечении. Поэтому мы измеряли рост людей (a), высоту пупка (b) и расстояние от головы до пупка (c). Затем в программе Microsoft Office Excel 2007 находили отношения этих величин (a/b, b/c) для каждого человека в отдельности, cреднее значение для группы людей одного возраста (a/b), сравнивали отношения с величиной золотого сечения (1,618) и выбирали людей с золотой пропорцией (приложение Б).

Результаты исследования мы представили в виде таблицы (таблица 3.1).

Таблица 3.1 – Соответствие пропорций человеческого тела золотому сечению у людей разного возраста.

Класс

Количество человек

Полученное среднеарифметическое

отношение

Количество людей с золотой пропорцией

1

11

1,701

0

5

14

1,652

0

9

19

1,640

2

11

8

1,622

1

Учителя

10

1,630

2

11 класс и учителя

62

1,626

3

Наглядно эти данные можно представить в виде диаграмм (приложения В и Г).

По результатам проведенного исследования можно сделать следующие выводы:

1. с возрастом у человека пропорции тела изменяются;

2. пропорции тела человека отличаются даже у людей одного возраста;

3. у взрослых людей пропорции тела приближаются к величине золотого сечения, но редко соответствует ему;

4. идеальные пропорции золотого сечения не применимы ко всем людям.

Следовательно, золотое сечение в пропорциях тела человека — это среднестатистическая величина, к которой приближаются пропорции тела взрослого человека. Только у некоторых людей пропорции тела соответствуют золотому сечению.

ЗАКЛЮЧЕНИЕ

Золотое сечение является мерилом гармонии в природе и в произведениях искусства на протяжении многих веков. Учение о золотом сечении получило широкое применение в математике, физике, химии, живописи, эстетике, биологии, музыке, технике.

Целью исследовательской работы было изучение золотого сечения, как идеальной пропорции строения человеческого тела.

Для достижения цели мы изучили литературу по теме исследовательской работы, познакомились с золотым сечением, с его построением, применением и историей; узнали математические закономерности в пропорциях тела человека; научились находить золотое сечение в пропорциях людей (приложение Д).

В практической части мы определяли соответствие пропорций человеческого тела золотому сечению, проверяли следующую гипотезу: пропорции каждого человеческого тела соответствуют золотому сечению.

Для проверки гипотезы мы измеряли рост людей и некоторые части тела у учащихся 1, 5, 9, 11 классов и учителей разного возраста.. Затем в программе Microsoft Office Excel 2007 находили отношения величин для каждого человека в отдельности, cреднее значение для группы людей одного возраста, сравнивали полученные отношения со значением золотого сечения и выбирали людей с золотой пропорцией.

На основании результатов проведенного исследования можно сделать следующие выводы:

1. с возрастом у человека пропорции тела изменяются;

2. пропорции тела человека отличаются даже у людей одного возраста;

3. у взрослых людей пропорции тела приближаются к величине золотого сечения, но редко соответствует ему;

4. идеальные пропорции золотого сечения не применимы ко всем людям.

Следовательно, золотое сечение в пропорциях тела человека — это среднестатистическая величина, к которой приближаются пропорции тела взрослого человека. Только у некоторых людей пропорции тела соответствуют золотому сечению. Наша гипотеза подтвердилась частично.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Васютинский, Н.А. Золотая пропорция / Н.А.Васютинский – М.: Мол. гвардия, 1990. – 238 с.

2. Ковалев, Ф.В.Золотое сечение в живописи: учеб. пособие/ Ф.В. Ковалев. — К.:Выща школа. Головное изд-во, 1989.—143 с.

3. Лукашевич, И.Г. Математика в природе /И.Г. Лукашевич. -Минск: Белорус. ассоц. «Конкурс», 2013. — 48с.

4. Мир математики: в 40т. Т.1: ФернандоКорбалан. Золотое сечение. Математический язык красоты /Пер.с англ. — М.:Де Агостини, 2014. — 160с.

5. Стахов, А.П. Коды золотой пропорции/А.П. Стахов. — М.: «Радио и связь»,1984. – 152с.

6. Тимердинг, Г.Е. Золотое сечение /Г.Е.Тимердинг; под ред. Г.М.Фихтенгольца; пер. с нем.- Петроград: Научное книгоизд-во, 1924. – 86с.

7. Урманцев, Ю.А. Симметрия природы и природа симметрии /Ю.А.Урманцев. — М.,Мысль,1974. — 229с.

8. Я познаю мир: Дет.энцикл: Математика /Авт.-сост. А.П.Савин и др.; худож.А.В.Кардашук и др. — М.: АСТ: Астрель, 2002. — 475с.

ПРИЛОЖЕНИЕ А

ЗНАЧЕНИЕ ЗОЛОТОГО СЕЧЕНИЯ

Рисунок А.1 – Более точное значение Ф

ПРИЛОЖЕНИЕ Б

СООТВЕТСТВИЕ ПРОПОРЦИЙ ЧЕЛОВЕЧЕСКОГО ТЕЛА ЗОЛОТОМУ СЕЧЕНИЮ

Таблица Б.1-Результаты измерения людей и вычисление среднеарифметических значений пропорций тела для учащихся 1, 5, 9, 11 классов и учителей

Класс

Рост (а)

Высота линии пупка (b)

Рассто-яние от пупка до головы (с)

а/b

b/c

Среднее арифме- тическое значение (a/b)

1

2

3

4

5

6

7

8

9

Золотое сечение

1,618

1,618

1

Андреев Владислав

1а

130

77

53

1,688

1,453

2

Грабцевич Дарья

1а

125

71

54

1,760

1,315

3

Ваванова Дарья

1а

127

74

53

1,716

1,396

4

Захаренко Родион

1а

124

74

50

1,676

1,480

1класс

5

Капориков Даниил

1а

133

79

54

1,684

1,463

1,701

6

Карсаков Захар

1а

120

71

49

1,690

1,449

7

Лазовый Максим

1а

128

75

53

1,707

1,415

8

Ласоцкая Анна

1а

125

76

49

1,645

1,551

9

Моргунова Мария

1а

116

66

50

1,758

1,320

10

Павлющенко Егор

1а

129

77

52

1,675

1,481

11

Раковский Александр

1а

128

75

53

1,707

1,415

12

Бахарева Ксения

5а

146

87

59

1,678

1,475

13

Бытковский Максим

5а

145

85

60

1,706

1,417

14

Жданович Виктория

5а

146

86

60

1,698

1,433

5класс

15

Климова Ксения

5а

155

95

60

1,632

1,583

1,652

16

Ларченко Евгения

5а

158

94

64

1,681

1,469

17

Листвягов Сергей

5а

143

87

56

1,644

1,554

18

Мухина Анастасия

5а

144

88

56

1,636

1,571

19

Падерина Анастасия

5а

151

91

60

1,659

1,517

20

Прочуханов Денис

5а

151

92

59

1,641

1,559

21

Савкина Анастасия

5а

140

87

53

1,609

1,642

22

Симакович Алевтина

5а

137

84

53

1,631

1,585

23

Сурганова Дарья

5а

150

92

58

1,630

1,586

24

Смоляров Владислав

5а

142

86

56

1,651

1,536

25

Тихинский Александр

5а

144

88

56

1,636

1,571

26

Аверков Алексей

9а

171

104

67

1,644

1,552

Продолжение таблицы Б.1

Учителя

54

Булай Е.И.

учит.

163

101

62

1,614

1,629

1,630

55

Волкова О.В.

учит.

164

100

64

1,64

1,563

56

Гриневская Н.А.

учит.

166

101

65

1,644

1,554

57

Гринченко Е.Б.

учит.

162

99

63

1,636

1,571

58

Киреенко А.С.

учит.

175

108

67

1,620

1,612

59

Стукалов Д.М.

учит.

165

101

64

1,634

1,578

11класс и учителя

60

Цедрик Н.Е.

учит.

158

96

62

1,646

1,548

61

Шкоркина Н.Н.

учит.

165

103

62

1,602

1,661

1,626

62

Яценко В.Н.

учит.

162

101

61

1,604

1,656

ПРИЛОЖЕНИЕ В

РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЯ ПРОПОРЦИЙ ТЕЛА У ЛЮДЕЙ РАЗНОГО ВОЗРАСТА

Рисунок В.1 – Результаты вычисления пропорций тела у учащихся 1 класса

Рисунок В.2 – Результаты вычисления пропорций тела у учащихся 5 класса

Рисунок В.3 – Результаты вычисления пропорций тела у учащихся 9 класса

Рисунок В.4 – Результаты вычисления пропорций тела у учащихся 11 класса

Рисунок В.5 – Результаты вычисления пропорций тела у учителей

ПРИЛОЖЕНИЕ Г

СРАВНЕНИЕ ПРОПОРЦИЙ ТЕЛА ЛЮДЕЙ РАЗНОГО ВОЗРАСТА

СО ЗНАЧЕНИЕМ ЗОЛОТОГО СЕЧЕНИЯ

Рисунок Г.1 – Сравнение средних пропорций тела людей разного возраста со значением золотого сечения

ПРИЛОЖЕНИЕ Д

ЭТАПЫ РАБОТЫ НАД ИССЛЕДОВАНИЕМ

а) б) в)

Рисунок Д.1 — Изучение литературы

а) б) в)

г) д)

Рисунок Д.2 — Проведение измерений учащихся и учителей

Рисунок Д.3 – Ввод и обработка полученных данных