Как составить и рассчитать пропорцию: онлайн калькулятор
Онлайн калькулятор пропорций
Формула пропорций
Пропо́рция — это равенство двух отношений, когда a:b=c:d
| средние | ||||||
| ╭ | члены | ╮ | ||||
| 1 | : | 10 | = | 7 | : | 70 |
| ╰ | крайние члены | ╯ | ||||
| 0,1 | = | 0,1 | ||||
Основные свойства пропорции
Произведение крайних членов равно произведению средних членов (крест-накрест): если a:b=c:d, то a⋅d=b⋅c
1 10 ✕ 7 70 1 ⋅ 70 = 10 ⋅ 7
Обращение пропорции: если a:b=c:d, то b:a=d:c
1 10 7 70 10 1 = 70 7
Перестановка средних членов: если a:b=c:d, то a:c=b:d
1 10 7 70 1 7 = 10 70
Перестановка крайних членов: если a:b=c:d, то d:b=c:a
1 10 7 70 70 10 = 7 1
Решение пропорции с одним неизвестным | Уравнение
1 : 10 = x : 70 1 10 = x 70
Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение
x = 1 ⋅ 70 10 = 7
Как посчитать пропорцию
Задача: нужно пить 1 таблетку активированного угля на 10 килограмм веса. Сколько таблеток нужно выпить, если человек весит 70 кг?
Составим пропорцию: 1 таблетка — 10 кг x таблеток — 70 кг Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение: 1 таблетка x таблеток ✕ 10 кг 70 кг x = 1 ⋅ 70 : 10 = 7 Ответ: 7 таблеток
Задача: за пять часов Вася пишет две статьи. Сколько статей он напишет за 20 часов?
Составим пропорцию: 2 статьи — 5 часов x статей — 20 часов x = 2 ⋅ 20 : 5 = 8 Ответ: 8 статей
Будущим выпускникам школ могу сказать, что умение составлять пропорции мне пригодилось и при расчёте процентов, и для того, чтобы пропорционально уменьшать картинки, и в HTML-вёрстке интернет-страницы, и в бытовых ситуациях.
Нахождение неизвестного члена пропорции | umath.ru
Пропорция — это равенство двух отношений.
Например, отношения 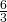 и
и 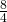
![\[\frac{3}{6} = \frac{8}{4}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-5a0a36c09173656b2d91ddd8cd6c040b_l3.png)
Эту пропорцию также можно записать так:
![\[3 : 6 = 8 : 4.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-ce1268e17da3f1d4ebc25f1291170842_l3.png)
В пропорции выделяют крайние и средние члены. Например, в пропорции 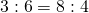 крайними членами являются числа
крайними членами являются числа 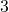 и
и 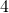
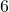 и
и 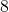 .
.Основное свойство пропорции
Если пропорция составлена верно, то верно следующее утверждение:
Произведение крайних членов пропорции равно произведению средних.
То есть если пропорция
![\[\frac{a}{b} = \frac{c}{d}\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-947c383783d4f9c72ec308b9b3863822_l3.png)
верна, то
![\[a\cdot d = b\cdot c.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-c680b242fd843bc131848b706d631c74_l3.png)
Онлайн калькулятор пропорций
Наш калькулятор вычисляет неизвестный член пропорции онлайн. Просто введите известные члены пропорции, а место для неизвестного оставьте пустым, и калькулятор выдаст ответ с подробным решением.
калькулятор пропорций с x
Вы искали калькулятор пропорций с x? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и калькулятор пропорций с дробями и иксом 6 класс, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «калькулятор пропорций с x».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как калькулятор пропорций с x,калькулятор пропорций с дробями и иксом 6 класс,онлайн калькулятор пропорций с дробями,онлайн пропорции,онлайн пропорция,онлайн решение пропорции,пропорции онлайн калькулятор,пропорции онлайн решение,пропорции онлайн решить,пропорции расчет онлайн,пропорции решение онлайн,пропорции решить онлайн,пропорция калькулятор онлайн,пропорция онлайн,пропорция решение онлайн,рассчитать пропорцию онлайн,решение онлайн пропорции,решение пропорции онлайн,решение пропорции онлайн калькулятор,решение пропорции с дробями онлайн калькулятор,решение пропорций онлайн,решение пропорций онлайн калькулятор,решение пропорция онлайн,решить онлайн пропорции,решить пропорции онлайн,решить пропорцию онлайн,решить пропорцию онлайн калькулятор,составить пропорцию онлайн калькулятор,считать пропорции онлайн. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и калькулятор пропорций с x. Просто введите задачу в окошко и нажмите «решить» здесь (например, онлайн калькулятор пропорций с дробями).
Где можно решить любую задачу по математике, а так же калькулятор пропорций с x Онлайн?
Решить задачу калькулятор пропорций с x вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Онлайн калькулятор: Золотое сечение
Калькулятор ниже находит параметры, соответствующие золотому сечению. Про само золотое сечение рассказано под калькулятором
Золотое сечение
ТипДлинный отрезокКороткий отрезокСуммарный отрезокТочность вычисленияЗнаков после запятой: 8
Длинный отрезок
Короткий отрезок
Суммарный отрезок
Золотое сечение
save Сохранить share Поделиться extension Виджет
Золотое сечение — термин, обозначающий деление отрезка на два в соотношении, при котором большая часть относится к меньшей также как весь отрезок относится к большей. Также употребляют термин деление в крайнем и среднем отношении.
Отношение это фиксированное, его можно найти. Представим, что b у нас единица. Тогда значение a должно равняться искомому отношению, и его надо найти — переименуем его в более привычное
Последнее есть квадратное уравнение. Его положительный корень:
и есть отношение золотого сечения. Число это иррациональное:
Для практических целей иногда используют приближение — большая часть равна 0,62 всей величины, меньшая — 0,38 (это видно, если ввести длину 1, и выбрать тип «суммарный отрезок» в калькуляторе сверху).
Золотое сечение известно еще со времен Евклида (ок. 300 лет до н. э.), и у него много забавных свойств, про которые можно почитать в: Википедии, например, к нему стремится отношение последовательных чисел Фибоначчи.
Для полноты ликбеза скажем, что почему-то считается, что объекты, содержащие золотое сечение, воспринимаются людьми как наиболее гармоничные. Ну а вот целая занятная статья, где золотое сечение находят буквально во всем.